|
|
|---|---|
Sperimentare la Fisica del Caos e dei Sistemi Complessi |
|
|
|
Imparare (oltre che fare seriamente ricerca) le leggi della Fisica alla base del Caos e dei Sistemi Complessi oggi è possibile grazie alle simulazioni interattive al computer. Queste ultime rivestono, per lo studio dei sistemi complessi, la stessa importanza che le osservazioni al telescopio hanno per lo studio dell'astronomia o che il microscopio e gli esperimenti con gli acceleratori di particelle hanno per lo studio della struttura della materia. |
|
L'unico modo di sapere come si comporterà un sistema fisico, biologico o sociale, composto da centinaia o migliaia di elementi interagenti - particelle, cellule, animali o individui - è infatti quello di simulare quel sistema al computer (realizzandone quindi quello che viene detto un "modello") e di osservare quello che succede: molto spesso, anche a dispetto della apparente semplicità degli elementi e/o delle modalità di interazione, si assisterà alla comparsa di comportamenti imprevisti e spesso sorprendenti che emergono spontaneamente dalla dinamica interna del sistema quando un dato "parametro di controllo" attraversa certe soglie critiche. |
|
Quì di seguito trovate, sotto forma di applets Java, alcune simulazioni da noi realizzate per mezzo della piattaforma software Netlogo, che offre all'utente finale la possibilità di interagire facilmente ed efficacemente con i parametri del sistema, visualizzandone l'evoluzione dinamica con una grafica accattivante e osservando in tempo reale l'effetto delle modifiche effettuate per mezzo dei vari pulsanti, cursori o menù a scelta multipla. A corredo di alcune simulazioni troverete dei riferimenti a testi divulgativi che approfondiscono gli argomenti trattati ed anche qualche filmato dimostrativo. |
|
Insomma, giocando con le simulazioni anche voi potrete essere ricercatori, anche se solo per un giorno... Buon divertimento! ************* Chi desiderasse vedere in anteprima un'introduzione più dettagliata su Caos e Sistemi Complessi può cliccare subito sull'immagine qui sotto per scaricare la presentazione (in formato .pps) |
|
| Nota: Le applets contenute in questa pagina richiedono la preinstallazione del Java Runtime Environment (Java 1.4.1 or successivi), che però non gira su Windows 95 o Mac OS 8 e 9. Gli utenti Mac devono avere OS X 10.2.6 o successivi e usare un browser che supporti Java 1.4. E' possibile scaricare l'ultima versione dei plugins Java direttamente dal Sun's Java site. | |
Un prototipo del Caos: La Mappa Logistica |
|
Letture consigliate sul Caos: - "Caos. La nascita di una nuova scienza" di James Gleick, BUR Biblioteca Univ. Rizzoli (collana Superbur scienza)
|
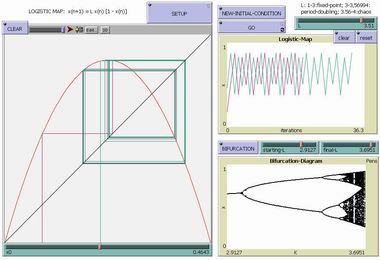
Cominciamo subito con la cosiddetta Mappa Logistica, uno dei sistemi dinamici più semplici in grado di mostrare un comportamento caotico estremamente complesso. Si tratta di una funzione ricorsiva, detta appunto "mappa", che trasforma un numero reale x(n) dell'intervallo [0,1] in un altro numero x(n+1) dello stesso intervallo secondo la formula iterativa x(n+1)=L*x(n)*[1-x(n)], dove L è un parametro di controllo, compreso tra 0 e 4. Dopo aver scelto la condizione iniziale x(0) (con il cursore in basso a sinistra) e un valore per il parametro L (cursore in alto a destra), premere il pulsante SETUP e poi il pulsante GO: la stessa evoluzione temporale della mappa, secondo due prospettive diverse, verrà mostrata nei plot a sinistra e a destra in alto. Diversi valori del parametro di controllo (secondo le soglie critiche indicate in alto a destra) condurranno a diversi regimi di comportamento (attrattori a punto fisso, cicli limite, attrattori caotici). E' possibile anche partire da una nuova condizione iniziale senza cancellare la traiettoria precedente, premendo l'apposito pulsante (NEW-INITIAL-CONDITION) senza ripremere SETUP. BIFURCATION disegna invece il Diagramma di Biforcazione, che mostra gli attrattori della dinamica in funzione dell'intervallo di valori di L scelto per mezzo dei due cursori. |
Generare un oggetto frattale: la Curva di Koch |
|
|
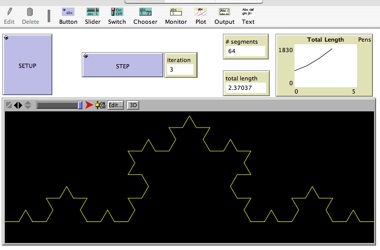
Vediamo adesso come generare un oggetto frattale, ossia un oggetto dotato di dimensione frazionaria. In questo caso si tratta della cosiddetta "Curva di Koch"o curva a "fiocco di neve", generata attraverso una procedura ricorsiva che consiste in una ripetizione delle seguenti istruzioni. Partendo da un segmento di determinata lunghezza: 1. dividere il segmento in tre segmenti uguali; 2. cancellare il segmento centrale, sostituendolo con due segmenti identici che costituiscono i due lati di un triangolo equilatero; 3. tornare al punto 1 per ognuno degli attuali segmenti. Partendo da un segmento, se ne ottengono quindi quattro (costituenti una linea spezzata) dopo la prima iterazione, 4x4=16 dopo la seconda e così via, generando al limite un elegantissimo frattale. Ingrandendo un qualunque dettaglio del frattale si ottiene ancora lo stesso frattale: in questo consiste la celebre proprietà di autosomiglianza dei frattali a qualunque livello di scala. |
L'Insieme di Mandelbrot |
|
- Vedi filmato sull'insieme di Mandelbrot |
L'insieme di Mandelbrot è uno degli oggetti frattali più famosi ed interessanti. Esso è definito come l'insieme dei numeri complessi c per cui non è divergente la successione definita da: z(n+1) = z(n)^2 + c ,con z(0) = 0. Se si rappresenta con colori diversi il comportamento di queste successioni per ogni punto del piano complesso (o almeno della porzione di quest'ultimo all'interno della quale è contenuto l'insieme di Mandelbrot), ecco emergere come per magia una figura estremamente ricca e frastagliata, simile ad uno scarabeo, che presenta affascinanti "paesaggi matematici" ad ogni scala di osservazione. Questa applet non è stata realizzata con Netlogo. Dopo aver impostato il parametro "Autopilot" su "Manual", occorre premere il pulsante GO! in basso e disegnare con il mouse delle finestre rettangolari ad ingrandimenti successivi per esplorare le meraviglie dell'insieme di Mandelbrot. |
Il Biliardo Caotico |
|
|
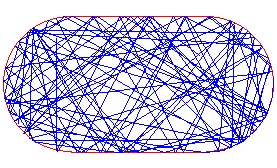
Una delle manifestazioni più immediate e allo stesso tempo più interessanti del Caos si ha nel gioco del biliardo. Su un normale tavolo da biliardo rettangolare non si manifesta alcun comportamento caotico nella traiettoria seguita dalla biglia. Essa è perfettamente prevedibile, ed un leggero cambiamento nella direzione iniziale del tiro non la altera in maniera sensibile. Ma su un tavolo da biliardo di forma simile a quella di uno stadio (ossia un rettangolo con i bordi smussati) le traiettorie delle biglie assumono un aspetto completamente diverso: la dinamica di un tavolo da biliardo a forma di stadio è infatti caotica e il sistema diventa estremamente sensibile alle condizioni iniziali. In questa applet è possibile partire da un biliardo di forma circolare, la cui dinamica è regolare, e "allungarlo" (modificando la variabile "Ratio") trasformandolo in un biliardo caotico (dove le traiettorie, dopo un sufficiente numero di passi, finiscono per riempire uniformemente il piano del biliardo - proprietà nota come "ergodicità"). |
Il Pendolo Semplice |
|
|
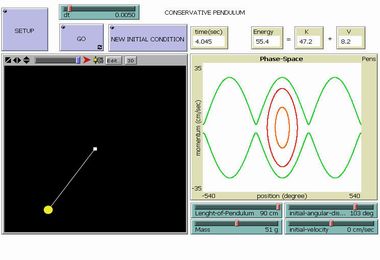
Reso celebre da Galileo, che per primo ne ha descritto correttamente le leggi dell'isocronismo, il pendolo semplice è costituito da una massa puntiforme sospesa ad un filo inestensibile e soggetta alla sola forza di attrazione gravitazionale. Nell'approssimazione di piccole oscillazioni esso rappresenta un tipico esempio di oscillatore armonico, la cui equazione del moto è lineare nella variabile incognita, e dunque produce una oscillazione la cui ampiezza è proporzionale allo spostamento iniziale dalla posizione di equilibrio. Se si trascurano - come avviene in questa simulazione - le forze di attrito, il pendolo semplice costituisce un sistema "conservativo", il che significa che l'energia cinetica K (legata alla velocità) e l'energia potenziale V (legata alla posizione) cambiano continuamente ma la loro somma si conserva. Se il pendolo si limita ad oscillare le sue traiettorie nello spazio delle fasi (posizione VS velocità o momento) assumono l'aspetto di curve ellittiche chiuse la cui area è proporzionale all'energia totale. Per valori elevati della velocità iniziale il pendolo può, però, anche compiere rotazioni complete attorno al suo punto di sospensione: in questo caso le traiettorie nello spazio delle fasi descriveranno curve aperte periodiche. |
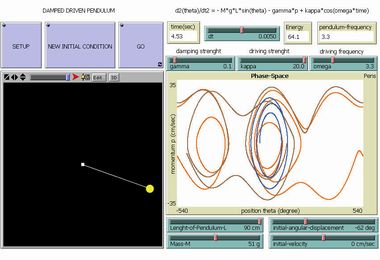
Il Pendolo Smorzato e Forzato |
|
Se si introducono nel modello precedente l'attrito (ossia una forza di smorzamento la cui intensità è regolata dalla variabile "damping strenght") e una forzante esterna sinusoidale (regolata dalle variabili "driving strenght" e "driving frequency"), l'equazione del moto del pendolo diventa non lineare e le prevedibili curve chiuse nello spazio delle fasi osservate nella simulazione precedente lasciano il posto a traiettorie più irregolari: in queste condizioni la sollecitazione a cui è soggetto il pendolo non è più proporzionale al suo spostamento e per certi valori dei parametri di controllo il pendolo diventa caotico, cioè il suo moto dipende criticamente dalle condizioni iniziali. |
|
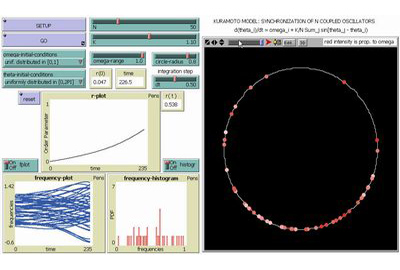
Il Modello di Kuramoto |
|
Alcuni filmati sul fenomeno della sincronizzazione: - Sincronizzazione di 5 metronomi su un'asse oscillante - Risonanza dovuta alla sincronizzazione dei pedoni sul ponte Millennium Bridge di Londra (vedi anche il Tacoma Bridge) - Sincronizzazione di una folla nella Ola Messicana (simulazione) Letture consigliate sulla Sincronizzazione: - "Sincronia. I ritmi della natura, i nostri ritmi" di Steven Strogatz, Editore Rizzoli
|
Consideriamo adesso non più uno ma numerosi (N) oscillatori accoppiati, ciascuno dotato di una propria frequenza naturale di oscillazione (le frequenze naturali sono delle forzanti esterne estratte da una distribuzione di probabilità uniforme o Gaussiana, e non variano nel tempo). Questi oscillatori possono essere più comodamente rappresentati come particelle in rotazione (senza collisioni) su una circonferenza di raggio unitario. Se gli oscillatori (o particelle) fossero isolati, ciascuno di essi tenderebbe a ruotare con la propria frequenza naturale. Ma, come ha mostrato per primo il fisico giapponese Yoshiki Kuramoto, l'accoppiamento sinusoidale di ogni oscillatore con tutti gli altri fa sì che, partendo da una distribuzione uniforme della particelle sulla circonferenza unitaria, al di sopra di una soglia critica del parametro di accoppiamento K il sistema diventi magicamente capace di "sincronizzarsi": in altre parole, nonostante gli oscillatori continuino ad essere soggetti alle proprie forzanti esterne naturali, le loro velocità istantanee di rotazione tendono ad assumere uno stesso valore (come mostrato dal plot in basso a sinistra). Questa transizione da uno stato uniforme ad uno sincronizzato può essere descritta per mezzo di un "parametro d'ordine" r(t), che assume valori prossimi a 0 nella fase omogenea e valori prossimi ad 1 in quella sincronizzata, come mostrato nel relativo plot (a sinistra, al centro). |
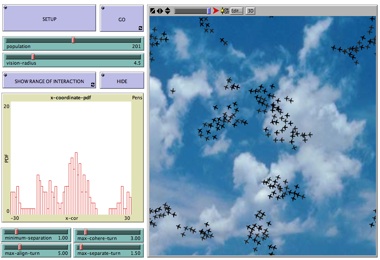
Come si formano gli Stormi di Uccelli |
|
|
- Vedi filmato su stormi e branchi di pesci |
La straordinaria proprietà di sincronizzare spontaneamente in qualche modo i propri elementi è caratteristica di molti sistemi complessi. Nel regno animale ne troviamo parecchi esempi, dal lampeggiare delle lucciole al canto dei grilli, dagli stormi di uccell ai branchi di pesci. In questa simulazione è possibile assistere alla formazione o alla distruzione di uno stormo semplicemente variando il "raggio di visione" dei singoli uccelli. Tra l'altro, questo è un esempio molto istruttivo per convincersi del ruolo fondamentale che il raggio di interazione gioca nell'ambito della fisica dei sistemi complessi, dove dominano i cosiddetti "sistemi con interazioni a lungo raggio", sistemi che spesso si trovano al confine tra ordine e caos (o, come si dice in inglese, "at the edge of chaos"). |
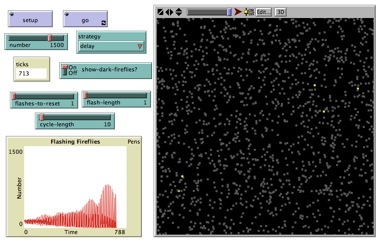
Sincronizzazione delle Lucciole (Fireflies) |
|
- Vedi filmato sulla sincronizzazione di lucciole reali |
Migliaia e migliaia di lucciole che, nelle lunghe notti tropicali, lampeggiano all'unisono immerse nella vegetazione che costeggia i fiumi, sono un altro esempio di sincronizzazione spontanea nel mondo animale. In questa simulazione potete influenzare la rapidità con cui le lucciole raggiungono lo stato sincronizzato, a partire da frequenze di lampeggiamento casuali, modificando tre parametri cruciali per mezzo degli appositi cursori. Il riquadro nero mostra le lucciole "accese" (in giallo) o "spente" (in grigio), mentre il plot in basso a sinistra mostra il numero di lucciole "accese" al passare del tempo: se sarete abbastanza pazienti da aspettare che il sistema si sincronizzi, assisterete a migliaia di lucciole che lampeggiano all'unisono, il che produrrà nel plot una curva con ampie oscillazioni periodiche. |
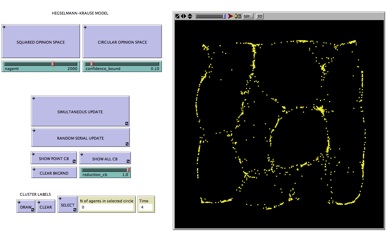
Dinamica di Opinioni di Hegselmann-Krause |
|
Letture consigliate sulla Sociofisica: - "L' atomo sociale. Il comportamento umano e le leggi della fisica" di Mark Buchanan, Editore Mondadori (Saggi)
|
Un divertente esempio di sincronizzazione nell'ambito sociale è costituito dal modello di dinamica delle opinioni (opinion dynamics) mostrato in questa simulazione. Se, semplificando, esprimiamo le opinioni di un gruppo di individui (agenti) con una coppia di numeri reali compresi tra 0 e 1 (le coordinate x e y dei puntini gialli in uno "spazio di opinioni" nero, quadrato o circolare), e fissiamo la regola che (fatta partire la dinamica simultanea o seriale) ad ogni istante l'opinione di un certo agente assuma il valore medio di tutte e sole le altre opinioni che si trovano all'interno di un intorno circolare (il cui raggio è espresso dal cosiddetto "confidence bound", regolabile per mezzo dell'apposito cursore), ecco che, al di sopra di una soglia critica del confidence bound, il sistema diventa in grado di sincronizzarsi, ossia - in questo caso - di raggiungere il consenso (convergenza dei punti gialli, cioè delle opinioni, verso un unico punto). Al di sotto della soglia critica, invece, il sistema converge verso uno stato stazionario dove coesistono diversi gruppi (clusters) di opinioni coincidenti e di dimensioni variabili (visualizzabili, queste ultime, premendo il tasto DRAW sotto CLUSTER LABELS). Le simulazioni di fenomeni sociali ispirate alla fisica stanno diventando così diffuse che è stato coniato il termine "Sociofisica" per definire questo nuovo settore di ricerca. |
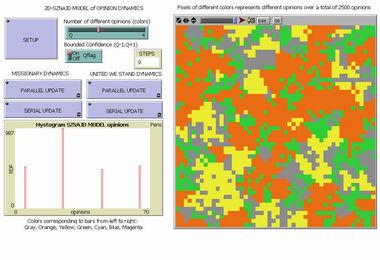
Dinamica di Opinioni di Sznajd-Weron |
|
In questo famoso modello di dinamica di opinioni, lo spazio quadrato diventa uno spazio fisico (una griglia) in cui risiedono gli agenti, le cui opinioni sono espresse da diversi colori. Ci sono due possibili dinamiche: in una (missionary), ad ogni passo ciascun agente modifica le opinioni dei suoi primi 4 vicini, che assumono la sua stessa opinione (cioè il suo stesso colore); nell'altra (united we stand), solo due agenti adiacenti con la stessa opinione possono convincere i loro 6 primi vicini, trasformandone ancora una volta il colore (l'opinione) nel proprio. L'utente può scegliere il numero di opinioni diverse con l'apposito cursore e, dopo aver eseguito il SETUP, lanciare una delle due dinamiche, con selezione parallela (tutti assieme) o seriale (uno per step) degli agenti. |
|
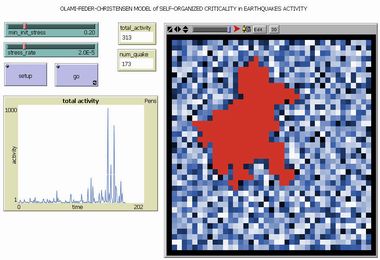
Criticità Auto-Organizzata nella Attività Sismica |
|
Letture consigliate sulla Criticità Auto-Organizzata: - "Ubiquità. Dai terremoti al crollo dei mercati: la nuova legge universale dei cambiamenti" di Mark Buchanan, Editore Mondadori (Oscar Quark)
|
Fenomeni cooperativi simili alla sincronizzazione regolano anche il comporamento di quei sistemi che si auto-organizzano nel cosiddetto "stato critico", come ad esempio la crosta terrestre. In questa simulazione la crosta è simulata da una griglia dove ogni casella esercita una certa pressione (stress) crescente su quelle adiacenti. Quando questa pressione supera una soglia critica, parte un processo a valanga (in questo caso un terremoto) e le caselle coinvolte si colorano di rosso: le leggi della criticità auto-organizzata (detta SOC, cioè Self_Organized Criticality) prevedono che una stessa causa iniziale, ancorchè piccola, possa dar luogo a terremoti di tutte le dimensioni, le cui entità dipende solo dalle "dita invisibili" delle correlazioni che attraversano il sistema. Questo stesso tipo di legge sembra regolare anche la produzione delle valanghe e degli incendi, lo scoppio delle guerre, l'estinzione delle specie, la diffusione delle mode e molti altri sistemi complessi che si trovano nello stato critico. |
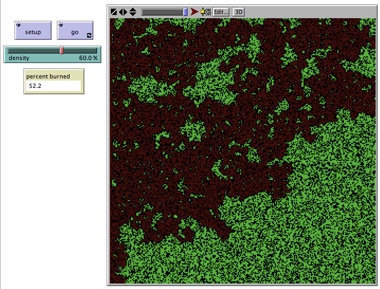
Soglie critiche nella propagazione degli Incendi |
|
Un semplice ma efficace esempio dell'esistenza di una soglia critica nei sistemi complessi, ossia di una soglia al di sopra della quale il sistema cambia improvvisamente e bruscamente il proprio regime di funzionamento, è proprio la propagazione degli incendi nelle foreste. In questa simulazione i puntini verdi sono alberi e il riquadro rappresenta un segmento di foresta soggetto ad un fronte di incendio rappresentato dalla sottile linea rossa lungo il lato sinistro. L'unico parametro di controllo del sistema è la densità degli alberi, modificabile per mezzo del cursore in alto. Dopo il SETUP, la pressione del pulsante GO avvierà l'incendio, ma il numero di alberi coinvolti dipenderà in modo cruciale dal superamento o meno di un valore critico della densità... |
|
Cooperazione tra Formiche |
|
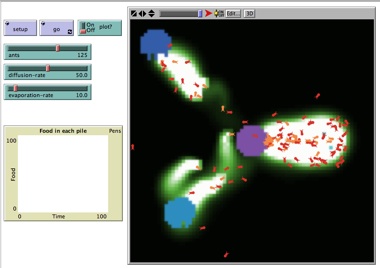
Ecco adesso un tipico esempio di cooperazione nel mondo animale. Le formiche, come noto, sono insetti con uno spiccato "senso sociale": quando una formica trova una fonte di cibo, lascia delle tracce di "feromoni" per aiutare le altre formiche a percorrere la stessa strada e rintracciare più velocemente il cibo (food). In questa applet, regolando con gli appositi cursori i tassi di diffusione e di evaporazione dei feromoni (colorati in bianco) emessi dalle formiche provenienti da un'uscita centrale (in viola), potrete osservare (nel plot in basso a sinistra) come varia la rapidità di esaurimento delle tre scorte di cibo (in blu) situate nei paraggi. |
|
Creare una Rete Complessa |
|
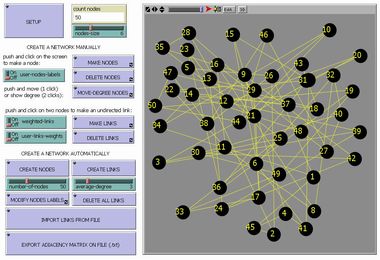
Molti sistemi complessi possono essere rappresentati per mezzo di Reti (Networks), cioè da oggetti costituiti solamente da nodi (che rappresentano gli elementi del sistema) e da links (che esprimono le relazioni tra questi elementi). Negli ultimi anni si è scoperto che il comportamento di queste reti non dipende dalla natura dei loro elementi (che possono essere particelle, cellule, individui, titoli azionari, computer, pagine web, etc...) ma solo dalla loro "topologia", cioè da come gli elementi sono collegati tra loro. In questa applet potete familiarizzare con questi importanti concetti, divertendovi a disegnare la vostra rete, scegliendo la posizione e il nome dei nodi e collegandoli a vostro piacimento per mezzo di links. |
|
Sincronizzazione di oscillatori su una Rete Complessa |
|
|
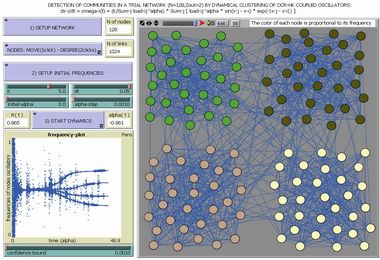
Se ad ogni nodo di una rete complessa associamo un oscillatore armonico, che stavolta interagisce solo con gli oscillatori corrispondenti ai nodi ad esso collegati, ecco che il fenomeno della sincronizzazione introdotto in precedenza può aiutarci a scoprire ed identificare le cosiddette "comunità" della rete, cioè quei gruppi di nodi più intensamente collegati tra di loro che con il resto del network. La rete test utilizzata in questa applet è una rete random costituita da 4 comunità, di 32 nodi ciascuna (per un totale di 128 nodi). Lanciando la simulazione è possibile osservare come le frequenze degli oscillatori associati ai vari nodi (espresse dall'utilizzo di diversi colori nel grafico che rappresenta la rete) tendano a sincronizzarsi tra loro solo all'interno di ciascuna delle 4 comunità predefinite, permettendone così l'identificazione. Il fenomeno è visualizzabile anche nel plot in basso a sinistra, dove si vede come, al passare del tempo, le frequenze istantanee degli oscillatori, inizialmente coincidenti, divergono lentamente e finiscono per stabilizzarsi su 4 livelli distinti, corrispondenti alle 4 comunità da identificare. |
Diffusione delle Epidemie su una Rete Complessa |
|
Letture consigliate sulle Reti Complesse: - "Nexus. Perché la natura, la società, l'economia, la comunicazione funzionano allo stesso modo" di Mark Buchanan, Editore Mondadori (Oscar Saggi)
|
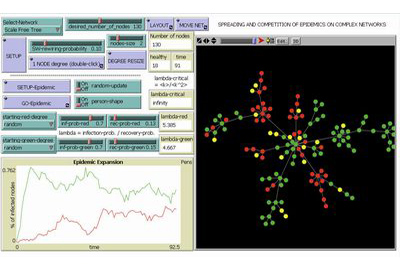
Un altra importante applicazione dei sistemi dinamici applicati alle reti complesse è rappresentata dalla diffusione epidemica dei virus, delle idee (memi) o delle mode. In questa simulazione occorre scegliere un tipo di rete (dal menù a tendina in alto) e il suo numero di nodi, dopodichè è possibile visualizzarla sullo schermo (col pulsante SETUP). La simulazione consiste nel far partire la dinamica (col pulsante GO-Epidemic) e osservare come due diversi virus o idee (rappresentati dai colori rosso e verde), partendo da due singoli nodi e diffondendosi ai nodi adiacenti, competano nel "contagiare" il maggior numero di nodi "sani", cioè quelli di colore giallo (da notare che un nodo, per poter essere contagiato da un certo virus o idea, deve prima "guarire", cioè ridiventare giallo). Tramite gli appositi cursori è possibile regolare sia la probabilità di "infezione" che quella di "guarigione" dei singoli nodi, e anche scegliere i nodi di partenza delle due epidemie (in modo casuale, o selezionando nodi con un alto o un basso numero di primi vicini - il cosiddetto "degree"), tutti fattori determinanti nell'assegnare la vittoria finale ad una di esse. Questi valori vanno ovviamente scelti prima dell'inizio della simulazione e fissati con la pressione del pulsante SETUP-Epidemic. |
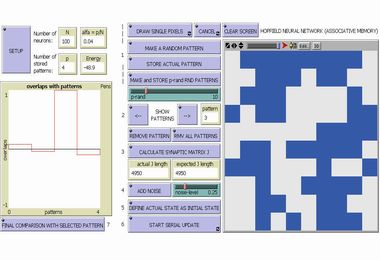
Reti Neurali: Memoria Associativa di Hopfield |
|
Letture consigliate sulle Reti Neurali: - "Reti neuronali. Dal perceptron alle reti caotiche e neuro-fuzzy" di Silvio Cammarata, Editore Etas (Collana Informatica)
|
Il nostro cervello è considerato il sistema complesso per eccellenza: miliardi di neuroni che interagiscono, attraverso sofisticate modalità elettrochimiche, per mezzo di un numero sterminato di connessioni (sinapsi). In questa simulazione una griglia (rete) di 10x10 neuroni artificiali "accesi" (blu) o "spenti" (grigi) e completamente connessi tra di loro (il celebre "Modello di Hopfield") ci permette di esplorare, in modo semplificato, le stupefacenti proprietà della nostra memoria associativa: già questa semplice rete neurale artificiale è infatti capace di rievocare un certo numero di forme, o "patterns", memorizzati nelle sue "sinapsi", a partire da uno stato iniziale rappresentato da una versione "perturbata" di uno di questi patterns. Il livello di "somiglianza" tra il pattern finale rievocato dalla rete e quello scelto inizialmente è quantificato per mezzo del cosiddetto "overlap", un numero reale compreso tra 1 e -1: un overlap pari a 1 significa che i due patterns sono identici, 0 che sono completamente scorrelati, -1 che sono l'uno il negativo dell'altro. |